Stress Distribution

Balloons on nails

This demonstration shows the effect of stress distribution.

Fig. 6-1: Balloon on nails

Place a balloon on a single nail and hold a thin wooden plate above the balloon and position the balloon as shown in Fig. 6-1a. Gradually transfer the weight of the plate onto the balloon. Before the full weight of the plate rests on the balloon, it will burst. This happens because the balloon is in contact with the very small area of the single nail, resulting in very high stress and causing the balloon to burst.

Now place another balloon on a bed of nails instead of a single nail. Put the thin wooden plate on the balloon and add weights gradually onto the plate as shown in Fig. 6-1b. It will be seen that the balloon can carry a significant weight before it bursts. It is observed that the shape of the balloon changes but it does not burst. Due to its changed shape, the balloon and hence the weight on the balloon are supported by many nails. As the load is distributed over many nails the stress level caused is not high enough to cause the balloon to burst.

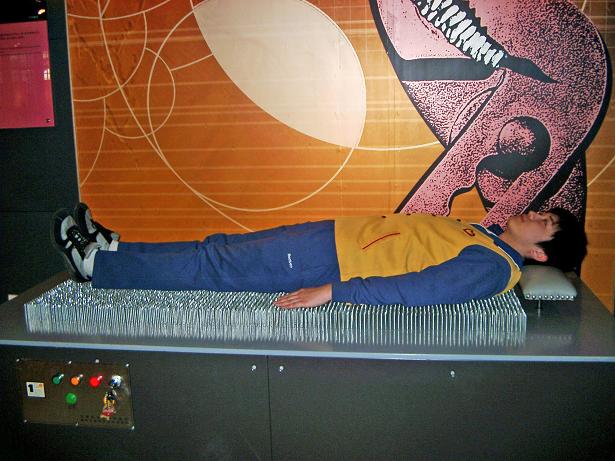
Fig. 6-2: A person lying on a nail bed

A similar example was observed at a science museum as shown in Fig. 6-2. A 6000-nail bed is controlled electronically allowing the nails to move up and down. When the nails move down below the smooth surface of the bed, a young person lies on the bed. Then the 6000 nails move up slowly and uniformly and lift the human body to the position shown in Fig. 6-2. If the body has a total uniform mass of 80kg and about two third of the nails support the body, each loaded nail only carries a force of 0.2 N or a mass of 20 grams. Thus the person is not hurt by the nails.

Fig. 6-3: Uniform force distribution

A similar but simpler demonstration can be conducted following the observation of the nail beds. Fig. 6-3a shows 49 plastic cups which are placed upside down and side by side. Place two thin wooden boards on them and invite a person to stand on the boards. The boards spread the weight of the person, 650 N, over the 49 cups, each cup carrying about 13 N, which is less than the 19 N capacity of a cup.

Uniform and non-uniform stress distributions

This demonstration shows the effect of non-uniform stress distribution.

Fig. 6-4: Uniform and non-uniform stress distributions (The model demonstration was provided by Mr. P Palmer, University of Brighton

Place a wooden block on a long sponge and apply a concentrated force at the centre of the block as shown in Fig. 6-4a. The sponge under the block deforms uniformly. If the concentrated force is placed at one end of the block as shown in Fig. 6-4b, the wooden block rotates with part of the block remaining in contact with the sponge and part separating from the sponge. It can be observed that the sponge deforms non-uniformly indicating a non-uniform stress distribution in the sponge.

Stress concentration

This demonstration shows the stress distributions of a sponge block model due to a compressive distributed load and a compressive concentrated load and Saint-Venant’s Principle.

Figure 6.A1: The model

The model comprises a piece of sponge on which a number of horizontal lines are marked, a T shaped stiff plate by which a distributed load or a concentrated load can be applied, and a base plate with two vertical metal tubes so that loads are applied vertically. Figure 6.A1 shows the components of the model and the sponge block before deformation.

When a distributed load is applied on the sponge as shown in Figure 6.A2a, it is observed that all the horizontal lines of the block remain horizontal. In this case, the stresses in the cross-sections of the sponge block are uniform and can be determined using the relationship  , where P is the total load and A is the area of the cross-section.

Figure 6.A2: Deformations of the sponge block due to uniformly distributed and concentrated loads

When a concentrated load is applied as shown in Figure 6.A2b, it can be observed that:

• Near of top end of the block where the concentrated load is applied, the lines form a pattern that radiates out from the loading point, indicating a radial stress configuration.
• At a distance from the loading point, the lines remain parallel to the base and appear the same as they did with the distributed load.

The second of the above two observations is an illustration of Saint-Venant’s Principle:

The stresses and strains in a body that are sufficiently remote from points of application of load depend only on the static resultant of the loads and not on the distribution of the loads [6.4]

The core of a section

The models demonstrate that the stress will be of the same type, compression or tension, throughout a section if a vertical load is applied within the core of the section.

Figure 6.A3: Rectangular and circular sections with their core areas

Figure 6.A3 shows rectangular and circular pieces of wood on which the core areas are marked in green on the tops of the pieces. The demonstrations show the effects when a vertical compressive load is applied within and outside of the core areas when the two wooden pieces are placed on a sponge blocks.

Figure 6.A4: A rectangular section subject to a vertical load

When an eccentric compressive load is applied perpendicular to the core area of the rectangular section as shown in Figure 6.A4a, it will cause both a uniform stress distribution and a linearly distributed stress distribution in the sponge block under the section. The uniform stress distribution is due to the action of the compressive load if it is applied at the centre of the rectangle while the linearly distributed stress is induced by the bending moment that is the product of the load and the distance between the point of the load and the centre of the rectangle. In this case, the maximum stress induced by the moment is smaller than the uniform stress. Thus all the areas of the wooden piece are subjected to compressive stress. In other words, the whole area of the rectangle is in contact with the sponge and there are no gaps between the wooden piece and the sponge.

When the load is applied outside of the core area, the linearly distributed stress will increase proportionally with the distance between the load point and the centre of the rectangle. In this case (Figure 6.A4b), the maximum stress due to the moment is larger than the uniformly distributed stress and this causes a separation between the wooden piece and the sponge resulting in a stress redistribution.

Figure 6.A5: A circular section subject to a vertical load

The same experiment can be repeated with the circular wooden section and similar results can be observed from Figure 6.A5. The experiments demonstrate that:

• When the load is applied within the core area, the stress applied on the wooden piece is all compressive, maintaining whole contact with the sponge (Figure 6.A5a).
• When the load is applied outside of the core area, separation occurs between part of the wooden section and the sponge with the contact area experiencing larger non-uniform stresses than the case when the load is applied within the core (Figure 6.A5b).

Flat shoes vs high-heel shoes

Fig. 6-5: Stresses exerted from flat and high-heel shoes
(Courtesy of Miss C Patel)

A woman wearing high-heel shoes or flat shoes will exert the same force on a floor but with significantly different stress levels. Fig. 6-5 shows a woman weighing 50 kg wearing flat shoes (a) and high-heel shoes (b). The stresses exerted by the shoes can be estimated as follows:

Flat shoes: The contact area of one of the flat shoes (Fig. 6-5a) is . Assuming the body weight is uniformly distributed over the contact area, the average stress is:

High-heel shoes : Assuming that half of the body weight is carried by the high-heels (Fig. 6-5b); each high-heel carries a quarter of the body weight. The area of the high-heel is . Thus the average stress under each high-heel is:

This shows that the stress under the heels of the high-heel shoes is about 60 times that under the flat shoes.

A typical adult elephant has a weight of about 5000 kg and the area of each foot is about . Thus the average stress exerted by an elephant’s foot is:

Elephants have large feet to distribute their body weight. The stress exerted on the ground by the foot of an elephant is much less than that under the high heel shoes.

The Leaning Tower of Pisa

Fig. 6-6: Lead blocks used to reduce the uneven stress distribution on foundation

The tilt of one of the world’s most famous towers, the Leaning Tower of Pisa, developed because of uneven stress distribution on the soil supporting the upper structure. The eight-storey tower weights 14,500 metric tonnes and its masonry foundations are 19.6m in diameter. If the stress were uniformly distributed, this would lead to an average stress of using Eq. 6-2. As the underlying ground consists of about 10m variabke soft silty deposits (Layer A) and then 40 m very soft and sensitive marine clays (Layer B), the Tower shows that the surface of Layer B is dish-shaped due to the weight of the Tower above it [6.3]. Thus the uneven stresses on the soft soil under the Tower caused the foundation to settle unevenly, making the Tower lean.

To redress the problem many large blocks of lead were placed on the ground on the side of the Tower where the settlement was least, as shown in Fig. 6-6. The new stress in the ground caused the firmer soil on this side of the tower to compress in turn preventing further leaning of the Tower and returning the Tower back towards the vertical.