Energy Exchange

A Moving Wheel

This demonstration shows the energy exchange between several common forms of energy, including gravitational potential energy, kinetic energy, energy loss due to friction and electro-magnetic energy.

Fig. 13-2: A moving wheel showing energy transformation

Two parallel, parabolic plastic tracks supporting an aluminum wheel are shown in Fig. 13-2. Three small magnets are placed on the perimeter of the aluminum wheel. Four batteries are located in the track support and an electro-magnetic field is also provided in the base support.

Place the wheel at one end of the tracks and release it. The wheel rolls towards the middle of the tracks with increasing speed as the potential energy of the wheel changes to kinetic energy. When passing the middle part of the tracks, the wheel speeds up due to a charge of electro-magnetic energy which is sufficient to compensate for the energy loss due to the friction between the wheel and the tracks. The wheel then moves upwards and the kinetic energy is converted to potential energy. When all the kinetic energy is converted, the wheel stops and then starts to roll back down the track for a new cycle of movement. The wheel will continue to roll backwards and forwards along the track as long as sufficient electro-magnetic energy is provided to compensate for the energy loss due to friction.

Collision Balls

This demonstration shows the use of the principles of conservation of energy and conservation of momentum.

Fig. 13-3: Collision balls

Fig 13-3 shows a Newton’s cradle which consists of five identical stainless steel balls suspended from the above and arranged in a row with each ball just touching its neighbour(s). When one pulls a ball back and releases it, it collides with the row of the remaining balls, ejecting one at the far end. If one pulls two balls and releases them, they eject two balls at the far end as shown in Fig. 13-3. Lifting and releasing three balls ejects three balls at the far end, and pulling four ejects four.

Fig 13-3 shows a Newton’s cradle which consists of five identical stainless steel balls suspended from the above and arranged in a row with each ball just touching its neighbour(s). When one pulls a ball back and releases it, it collides with the row of the remaining balls, ejecting one at the far end. If one pulls two balls and releases them, they eject two balls at the far end as shown in Fig. 13-3. Lifting and releasing three balls ejects three balls at the far end, and pulling four ejects four.

 or 

Conservation of energy requires:

 or 

Squaring the first equation and subtracting the second equation leads to:

 or 

As  ,  . This shows that after collision the first ball will be at rest [13.5, 13.6].

Now consider the case of several balls. Let  be the total mass of the balls launched with velocity  and  be the total mass of the balls ejected with velocity  . Noting that after collision,  becomes stationary, i.e.  and using conservation of momentum and conservation of energy gives:

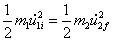
Squaring the first equation and subtracting  times the second equation gives:

This equation shows that the number of balls ejected is equal to the number of balls launched if all the steel balls are the same size, as shown in Fig.13-3.

Dropping a Series of Balls

This model gives an entertaining demonstration of conservation of energy.

Fig. 13-4 shows four rubber balls of different sizes placed together using a plastic bar passing through their centres with the smaller balls resting on the larger balls.

When the balls are lifted vertically for a distance of about 0.15 m from a desk and then released, the smallest ball rebounds to hit the ceiling which is over two metres above the desk. This observation can be explained using either the principle of conservation of energy or the princile of conservation of momentum.

The total mass of the four balls is 120 grams and the mass of the smallest ball is 5 grams. The gravitation potential energy of the balls before dropping them is estimated to be:

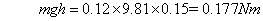
After the impact of the largest ball on the desk, the three larger balls bounce up almost together about 0.03m. According to the conservation of energy, the total gravitational potential energy before and after impact should be the same if no energy loss takes place, i.e.

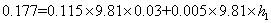
From the above equation, the predicted bounce height of the smallest ball is 2.92m. Actually there is some loss of energy due to the impacts between the largest ball and the desk and between the adjacent balls, so the smallest ball would not bounce quite as high as 2.92 m.

This example can also be analysed using the principle of conservation of momentum.

Roller Coasters

Fig. 13-5: Roller Coasters

Fig. 13-5a shows a roller coaster which is raised from ground level to the top of the first tower using mechanical energy. This builds up a reservoir of potential energy in the coaster.

When the coaster is released at the top of the tower, it moves forward and down, the potential energy being quickly converting to kinetic energy and the speed of the coaster increasing accordingly. The speed reaches its maximum when the coaster reaches the lowest point between two adjacent towers. The coaster then moves up to the next tower, the kinetic energy changing back to potential energy, and the speed of the coaster reduces as its potential energy increases. The rest of the towers, dips, twists and turns of the ride, serve to change the energy of the coaster back and forth between potential energy and kinetic energy (Fig. 13-5b).

During the motion, some energy will be lost due to friction and, for this reason, the first tower must be higher than all the other towers so that sufficient energy is provided to overcome the energy loss.

A Torch Without a Battery

Fig. 13-6: An environmentally friendly torch

Torches are normally powered by batteries. However, Fig. 13-6 shows an environmentally friendly torch which works on the principle of energy exchange.

When one shakes the torch, the strong magnet at the far right in the body of the torch (Fig. 13-6) moves and passes through electrical wires backwards and forwards and produces an electric current. Part of the kinetic energy generated by the magnet is converted to electric energy. The electric energy then changes into chemical energy through the electronic circuit and is stored in an internal storage cell. When a user switches on the torch, the chemical energy in the storage cell converts to electric energy and the electric energy changes to light energy in the bulb.